Hello, AlKon! 2025 Open Contest

전날 오랜만에 과음을 했더니 새벽에 눈이 떠져서 6시부터 놀다가 백준에 들어왔더니 아침부터 열리는 오픈콘이 있길래 참여했습니다.

 

어느 학교인지도 모르고 쳤는데 건국대 동아리 대회네요.

 

아직 문제가 공개되지 않아 기억에 의존해서 작성했습니다. 문제 공개 후 오류가 있다면 수정하겠습니다.

문제별 풀이가 적혀있으니 스포에 유의해주세요.

 

A. 새천년관

문제 조건을 만족하는 가장 짧은 문자열은 "nkugwan" 입니다. gwan에 k가 들어가는 줄 알고 한번 틀렸습니다🤣

B. 비밀번호

{(1,2), (2,1), (2,3), (3,2)} 와 {(1,1), (1,3), (3,1), (3,3)} 은 판을 돌리면 같은 위치이므로 경우의 수가 동일합니다.

 

(1,2)에서 시작하면 (1,1)과 (1,3)을 둘 다 지나는 것이 불가능합니다.

또는 3x3 체스판이라고 생각하고 첫 칸부터 교차로 검은색, 흰색을 칠해보면 검은 칸이 5개, 흰 칸이 4개인데 한번 이동할 때마다 색깔이 바뀌기 때문에 흰 칸에서 시작하면 모든 칸을 지나는 것이 불가능합니다.

 

(2,2)에서 시작하면 상하좌우 중 하나를 고르는 게 4가지, 고른 위치에서 양옆 중 어느 쪽을 가도 가능하므로 x2 해서 총 8가지의 경로가 존재합니다.

(1,1)은 예제에서 줘서 안해보고 그냥 냈습니다. 대회 끝나고 그려보니 8가지네요.

C. 건덕이의 돌탑

예제가 딱봐도 n*(n+1)/2처럼 생겼길래 예제 출력 해보고 찍었습니다.

실제 최적 해는 (1~n-1)을 2번 위치에 옮기고 n을 3번 위치에 옮기기, (1~n-2)를 1번 위치에 옮기고 n-1을 3번 위치에 옮기기, ... 를 반복하면 (n + (n-1) + ... + 1) = n * (n+1) / 2번의 이동이 필요합니다.

D. 안정적인 구간

길이가 2인 구간 [x, x+1] 이 문제 조건을 만족하지 않으려면 arr[x] > arr[x+1]이어야 합니다.

따라서 전체 구간이 문제 조건에 위배되려면 arr[1] > arr[2] > ... > arr[n]이어야 합니다.

그런데 arr[1] > arr[2] > arr[3] 이라면 arr[2]가 세 값의 중앙값이므로 문제 조건을 만족합니다.

따라서 n = 2, arr[1] > arr[2]인 경우만 빼고 항상 가능합니다.

E. 마스코트 정하기

(1)

1을 기준으로 왼쪽과 오른쪽을 전부 날려버리면 되므로, 답은 최대 2입니다.

만약 전체 구간에서 1이 절반 이상 등장했다면 답은 0이고, 그렇지 않다면 답은 최소 1입니다.

따라서 답이 1인 경우만 판별해주면 됩니다.

 

(2)

arr[1] ~ arr[k]까지 등장한 1의 개수를 셌을 때, 전체 구간의 절반 이상이 1인 k가 존재하는지 확인합시다.

만약 존재한다면 오른쪽 나머지 구간을 날려버리면 됩니다.

마찬가지로, arr[n]부터 한 칸씩 내려오면서 동일한 작업을 반복합니다.

위의 작업은 O(n)에 가능하며 만족하는 k가 하나라도 존재한다면 답은 1, 하나도 존재하지 않는다면 2입니다.

 

(3)

만약 (1 < x < y < n) 을 만족하는 x, y에 대해 [x, y] 구간을 날렸을 때 문제 조건을 만족한다고 가정합시다.

그렇다면 남은 [1, x-1], [y+1, n] 구간을 합쳤을 때 1이 절반 이상이라는 것을 의미합니다.

그런데 만약 왼쪽과 오른쪽 구간이 전부 1이 절반 이상이 되지 못한다면, 두 구간을 합쳤을 때도 1이 절반 이상이 되는 것이 불가능합니다.

따라서 왼쪽과 오른쪽 중 적어도 하나는 1이 절반 이상이고, 그 구간만 남기고 반대쪽 구간을 날려버려도 성립합니다.

그런데 이 케이스는 (2)에서 이미 확인하고 있기 때문에 추가적으로 확인해주지 않아도 됩니다.

 

왼쪽과 오른쪽의 평균은 절대 max(왼쪽, 오른쪽) 보다 클 수 없다는 관점으로 해석했을 때

https://www.acmicpc.net/problem/17594

이 문제와 아이디어가 동일한 것 같습니다.

F. 오름차순 최단 경로

(1)

2번 노드가 문제 조건을 만족하려면, 반드시 1 -> 2 인 간선이 있어야 합니다. 그렇지 않다면 다른 노드를 통해서 와야 하므로 반드시 해당 노드가 더 앞에 오게 됩니다.

 

(2)

3번 노드가 문제 조건을 만족하려면 반드시 1 -> 3 또는 2 -> 3인 간선이 있어야 합니다. 그렇지 않다면 (1)과 동일한 이유로 불가능합니다.

 

(3)

이걸 확장하면 2 이상의 임의의 x에 대해 (1 ~ x-1) -> x 인 간선이 최소 하나는 반드시 존재해야 합니다.

 

위상정렬 같은 것을 의도하고 출제된 문제인 것 같은데, 위의 조건을 체크하는 가장 쉬운 방법은 그냥 b가 2~n까지 최소 한 번씩 전부 입력으로 들어오는지 확인하면 됩니다.

int main() {
    fastio;
    ll n, m;
    cin >> n >> m;
    vector<int> pos(n+1);
    for(int i = 0; i < m; i++){
        int a, b;
        cin >> a >> b;
        pos[b] = 1;
    }
    for(int i = 2; i <= n; i++){
        if(pos[i] == 0){
            cout << "NO";
            return 0;
        }
    }
    cout << "YES";
    return 0;
}

G. 젓가락으로 메추리알 집기

(x, y) 위치를 젓가락으로 집었다고 해봅시다.

만약 메추리알이 (x-1, y), (x+1, y), (x, y-1), (x, y+1) 중 한 위치에 있었다면 메추리알이 움직입니다.

그렇지 않다면 메추리알은 자기 자리에 그대로 있습니다.

따라서 (x, y) 위치를 집었을 때 메추리알을 잡지 못했다면, 인접한 4칸에는 반드시 메추리알이 없다는 것을 알 수 있습니다.

 

이를 활용하면, 전체 칸을 체스판처럼 흑백으로 칠했을 때 흑 / 백 중 한 가지 색깔의 칸만 전부 확인하면 메추리알을 반드시 잡을 수 있다는 것을 알 수 있습니다.

 

최대 쿼리 횟수가 ⌊x * y / 2⌋ 이기 때문에 (x + y) % 2 = 0인 칸을 체크하면 가로 세로 길이가 둘 다 홀수일 때 최대 쿼리 횟수를 초과한다는 점을 주의해야 합니다.

H. 인수분해 정렬

인접한 두 칸 x, x+1에 대해 arr[x] * arr[x+1] = t 라고 합시다.

(1)

t가 1이거나 소수라면 a * b = t를 만족하는 (a, b) 가 (1, t) 로 유일하므로, 서로 바꿀 수 없습니다.

 

(2)

만약 그렇지 않다면 (합성수라면) 1보다 큰 두 자연수 a, b에 대해 a * b = t를 만족하는 (a, b)가 반드시 존재합니다.

이때 t = a * b = 1 * t 이므로 처음 상태에 관계없이 최대 두 번의 조작으로 arr[x] = t, arr[x+1] = 1이 되도록 할 수 있습니다.

 

(3)

만약 어떤 x에서 (2) 조건을 만족했다면, arr[x] = t, arr[x+1] = 1로 변환합니다. 그렇다면 arr[x-1] * arr[x] = arr[x-1] * t이므로 이 수는 반드시 합성수입니다. 따라서 arr[x-1] -> arr[x-1] * t, arr[x] = arr[x+1] = 1 로 변환할 수 있습니다.

이걸 반복해서 적용하면 아무 x에서나 위의 조건을 만족했다면 arr[1] = (arr[1] * arr[2] * ... * arr[x+1]), arr[2] = ... = arr[x+1] = 1로 만들 수 있습니다.

 

(4)

그런데 (2)에서 arr[x] = 1, arr[x+1] = t가 되도록 만드는 것도 항상 가능합니다.

따라서 (3)을 한번 수행한 다음에, arr[1]부터 다시 거꾸로 올라가면서 연산을 반복 적용하면 최종적으로 arr[n]을 제외한 나머지 모든 수를 1로 만드는 것이 가능합니다.

 

따라서 (2)를 만족하는 칸이 하나라도 존재하거나, 처음부터 배열이 비내림차순으로 저장되어 있었다면 전체 배열을 비내림차순으로 만드는 것이 항상 가능하고 그렇지 않다면 불가능합니다.

 

후기

 

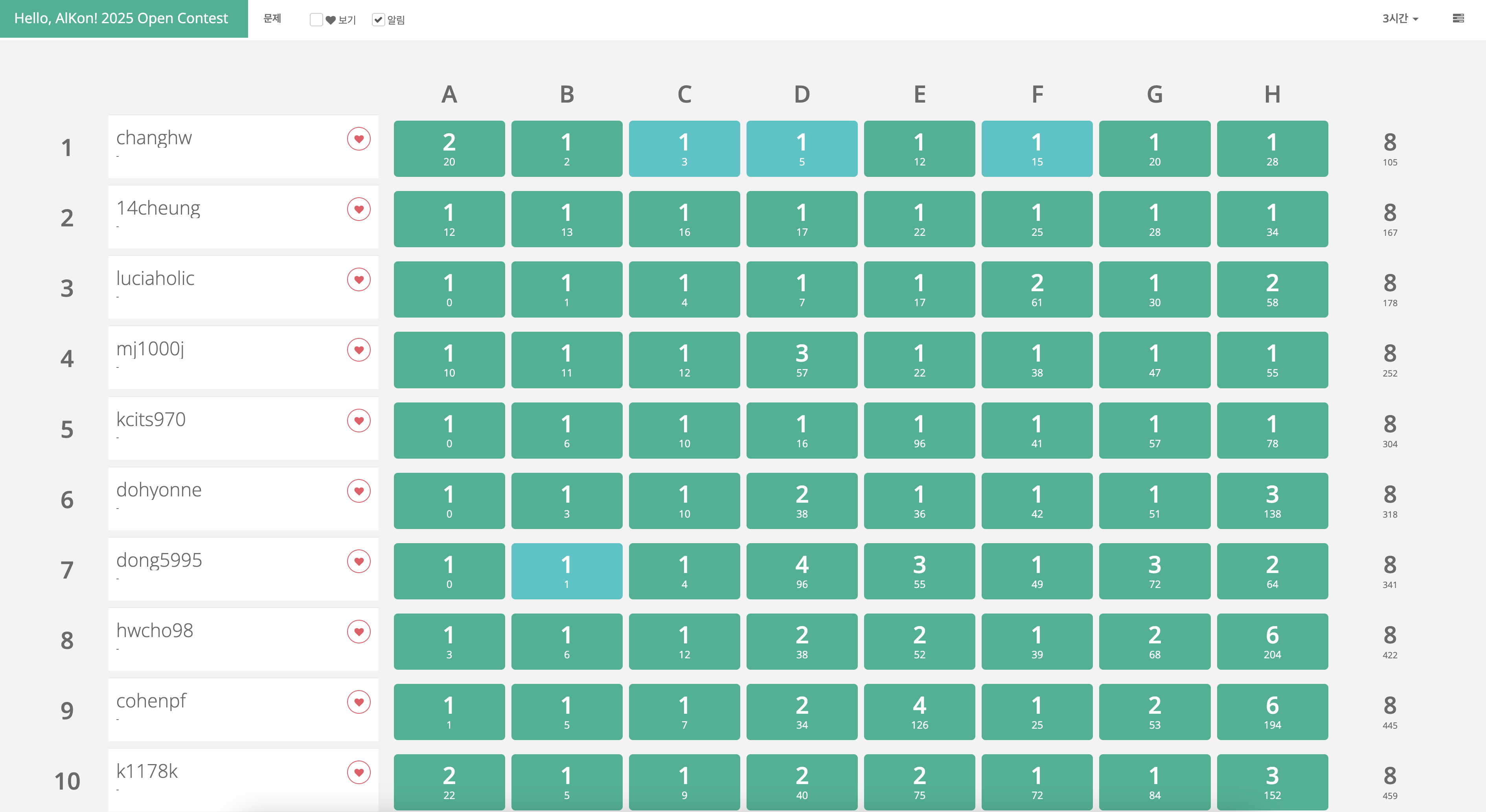
대회에 대한 아무 정보 없이 그냥 오픈콘이 열리길래 쳤는데, 아침이라 그런지 고인물 분들이 안 계셔서 빈집털이하고 1등 찍었습니다.

2등분이 A번을 12분에 풀고 H번을 34분에 푸셨는데 정각에 시작하셨으면 25분 컷이라는 얘기라서 확실히 빈집털이가 맞는 것 같습니다.

대회 1등은 처음이라서 얼떨떨하고 신기하네요.

 

그리고 A번만 한번 틀렸습니다. A번이 제일 어렵다

 

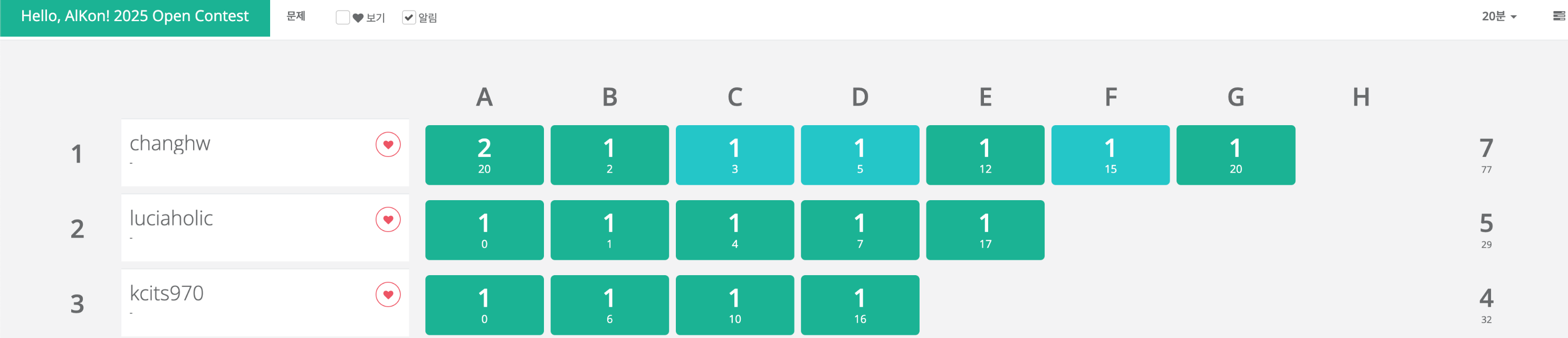
7솔 시점에서 2등이 5솔이고 3등부터 4솔이였는데 이런 경험은 앞으로도 절대 못하지 않을까 싶습니다. ㅋㅋㅋ

 

ps에 익숙하지 않은 사람들을 위한 난이도로 출제되었다고 들었는데 취지에 걸맞게 어려운 자료구조가 필요한 문제 없이 8문제 전부 해 구성이나 애드혹 문제들이라서 너무 재밌었습니다. 역시 애드혹이 최고의 태그죠